返済計算(4)−繰上返済

ローン返済のCalcでの計算はいかがでしょうか。
ここまでで、すでに下記のような内容を見てきました。

1. 元利均等返済計算
2. 元金均等返済計算
3. 繰上返済計算
4. 残額計算
5. Calcでの元利均等返済計算
6. Calcでの繰上返済計算

もうここまでできれば、Calcの重要な機能を使っています。
Calcの導入例として、あとは、使用したシートを使い倒してしまいましょう。

変動利息に対応する

Calcを使えば、利息が変わっても計算は簡単です。
固定の利息の代わりに、都度利息を指定するだけです。
こういうのは、用途限定ソフトで対応するのは大変ですが、Calcなら、計算に受け渡す利息を変えるだけです。
ということで、新しい計算表を作りましょう。
説明は抜きに、下記のような計算シートを作ります。

	A	B	C	D	E	F	G	H	I	J	K
1	元金	40000000
2	当初年利	1.5%
3	当初月利	=B3/12
4	固定返済額	=B1*B3*(1+B3)^420 /((1+B3)^420-1)
5
6	月	年利	月利	通常残高	繰返残高	通常支払額	繰返支払額	固定返済額	繰返額	通常利息分	繰返利息分
7	0	=B2	=B7/12	=B1	=B1
8	=A7+1	=B7	=B8/12	=D7-F8+J8	=E7-G8+K8	=F7+H8	=G7+H8+I8	=B4	空白	=D7*C8	=E7*C8

すこし目立っている固定返済額の右側の数式は、 元利均等返済の項で最初に求めた数式です。 この表を作成したら、A8:K8を選択し、420月までドラッグ&ドロップすれば、素材としての表は完成します。
ここまでの画面は下記のような感じです。

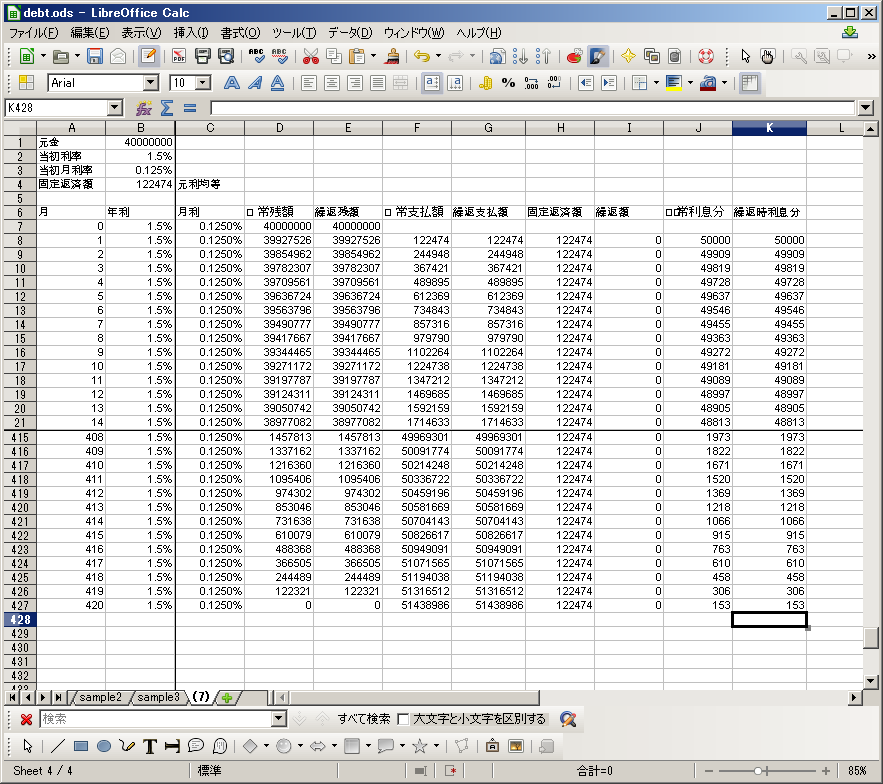
シートの上側が常時表示されるように設定していますが、こういう詳細は、後で少しずつ書いてゆくので、 あまり気にしないでくださいね。
最初は、金利を35年間1.5%で固定しています（こんな条件で貸すところはないか？）。
理由は、元利均等返済の金額計算を検証するためです。
金利はあとから変えられるようになっています。

420ヶ月目（35年）まで計算したところで、残額がゼロになり、返済が終わっていることに気付きます。
元利均等返済の項で最初に求めた数式は、正しいようですね。
しかし、正式な計算は、貸した側が提示するものです。
大きな差がでていたら、自分の計算間違いを疑い、次に、貸す側の計算を疑いましょう。
式は、どこからか引用したものではなく（どこかにあるでしょうが）、自分で導いたものなので、 公開するのは、躊躇しましたが、こうやって確かめると、間違ってはいないようで、少しほっとします。
こうやって、自分で求めた結果を検証できるのも、Calcを使う醍醐味のひとつです。

これを、グラフにしてみました。下記参照ください。

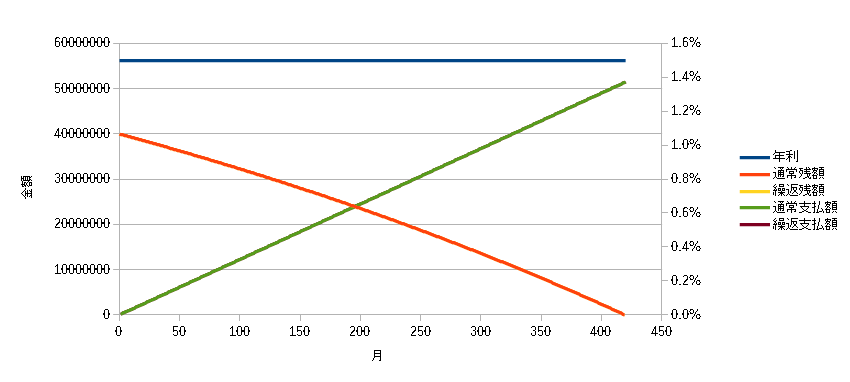
こうやって見てみると、1.5%の利率で35年返済というのは実にお得な条件ですね。
実際にあるかどうか分かりませんが、あるのなら、かなりお得です。
ただし、利息が変動する場合はどうなるか。
それは、これからシミュレーションしてみましょう。

利息が低いというのは、デフレの状態にあるということです。
皆がものを買わないので、物価が上がらないという状態です。
ですから公定歩合を低くして、金利を抑え、借金してまで買ってもらおうというのが、低金利政策です。
しかし、情勢が変わってインフレになったらどうなるか。
インフレになったら、資産の価格が上がるので、借金してまで不動産でも購入したら得かもしれません。
不動産価格がどんどん上がったらもう二度と買うチャンスがないのですから。
そう思いながらバブルで嵌った人も多いでしょうから、こればかりは何ともいえません。
金融資産のトレードは、読み誤りに気付いた時点で撤退ですが、不動産ローンは簡単に撤退できません。
この先どうなるのか、悩みどころではありますが、見通しを立てるのは必要です。

ということで、この先インフレになったとして、利率を最高で5%になるまで、変動させてみましょう。
利率を上げると、返済額が増えますから、利率改定の都度、返済額を増やしていることにも注目してください。

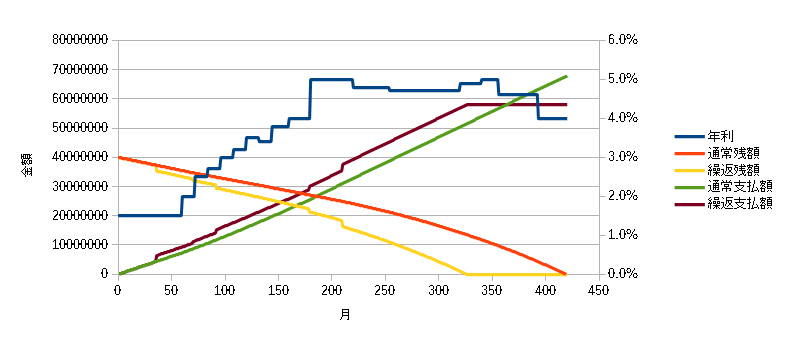
利率は、階段状の線で表されています。
超低金利の変動利息で借り入れて、従前の一般的な利息に上がっていったらどうなるのか。
対抗策は、繰上げて返済していくしかありません。
繰上げて返済すると、黄色の線のようになって、早く返済が終り、返済総額も少くなります（茶色）。
緑色が、繰上返済なしの場合の、支払額です。右上の端の値が、総支払額になります。
それでも、1.5%の金利で借り続けた場合と比較すると、とんでもなく多いですね。
また、下のグラフは、金利の変化に伴う、毎月の返済額の、シミュレーションです。
金利が変わる都度、残期間での元利均等払いの金額を毎月の返済額としています。

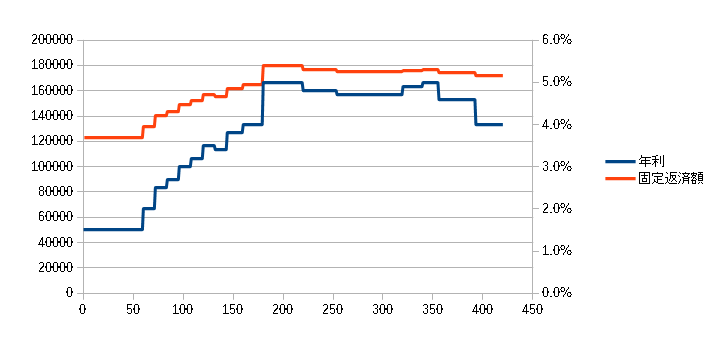
1.5%のときの返済額が12万円ちょっとだったのに対し、5%では、18万円近くなっています （残高と残期間により利率が一定でも同額にならないことに注意）。
これに耐えられる作戦を立てずに、現在の利率でギリギリの予算を立てるのは自殺行為と云えます。
借入額が低くなる安価な物件にするなり、いざというときのために積み立てるなり対応策が必要です。
こうして、予測を見誤った場合の心の準備をしておくことが重要です。

＜前に戻る｜次に進む＞

戻る

---