創造するコンテンツと技術習得を重視しよう
複利計算
複利計算は、前のページで簡単に説明しましたが、簡単に振り返ります。
複利計算は、利息にも利息がついて膨れ上がるという条件の計算方法です。
年間の利息(年利)をrとし、借入金をDとします。
そして、j年後の残金をdjとすると、
残金は、下記のようになります。
d1=D(1+r)
d2=d1(1+r)=D(1+r)2
.....
dj=dj-1(1+r)=D(1+r)j
このように、べき乗計算となり、時間が経過するほど、借金の膨れ方が大きくなります。
利息は、パーセントではなく、普通の割合であることに注意してください。
試しに年利5%の場合を計算すると、1+r=1.05なので、100万円借り入れて10年放置すると、
1,628,895円になります。
年利が15%とかになると、4,045,558円という恐ろしい額になります。
これが複利というものです。
元利均等返済の計算
複利の場合は、放っておくと、雪だるま式に残金が増えてゆくので、
残金が増えないように、利息を超える返済を続けることが必須です。
一括返済の契約もあり得ますが、そのような契約では、貸した側が回収不能になるリスクが
大きいので、なるべく、回収不能にならないような条件で貸し付けるのが普通です。
なるべく計画的に、コンスタントに、かつ、利息による収益が大きくなるような貸借契約になる
ことが多いでしょう。
これを書いている2014年6月時点では、異常な低金利が続いていますが、経済状況の変化により、
金利は、簡単に上がります。
元に十数年前は、3.5%でも史上空前の低金利と呼ばれていました。
それ以前は、6%という金利も普通のことでした。
物価上昇が見込まれる場合には、金利が高くなるので、今から先は金利が上がるかもしれませんね。
それはそれとして、元利均等返済の計算をみていきましょう。
数式が多いので、苦手な方は、ひととおり眺めたらCalcで計算するところまで、飛んでください。
各月の残高の変化は下記のようになります。

但し、

上記の残高変化を元に、元利均等の返済額を計算してみます。
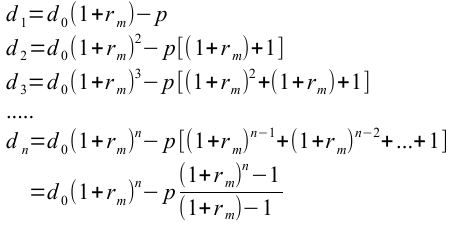
ここで、最終月に返済が終了するdn=0という条件から、
以下の毎月の返済額の式が求められます。
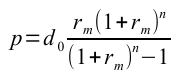
ここで、使用した記号は以下の通りです。

以上の式は、あとで検証してみましょう。
少し面倒ですが、以上で、元利均等返済条件での毎月の返済額が計算できます。
これには、恐ろしいボーナス月の特別返済が入っていません。
何があってもボーナス月には加算できるんだ、という自信があれば、それも手ではありますが、
ボーナス月の加算は、返済不能(デフォルト)のリスクを高めます。
<前のページに戻る| 次を読む| インデックスに戻る>