前回のシリーズ

マイナーオーディオ講座として、最初のシリーズでは、バスレフ型のシステムを中心とした箱について議論しました。
なるべく数式は使わないことにしたのには、意味があります。
その理由は2つあって、ひとつは、数式そのものが難しい場合があることです。
バスレフの動作を語るのに、運動方程式は必須ですが、運動方程式そのものを日常取り扱う人は稀なようです。
このため、学校では教わったものの、単位をとった、あるいは、受験をくぐり抜けた瞬間に忘れてしまい、 そのままお蔵入りになった人は少くないように思います。
また、自分の文書集は、運動方程式で記述しており、同じことを書く必要もないと考えました。

もうひとつの理由は、公式を使いたくない、ということです。
最近の大学の状況は分かりませんが、かつては、公式を使うには、厳格な条件を求められました。 そして、その厳格な条件を満たすかどうかを判断するためには、相当な知識を求められました。
このため、公式を使うには、相当な時間を使い、頭を使う必要がありました。

しかし、安易に公式を使うと、本質が見えなくなってしまいます。
このために、公式を使うことはなるべく避けようということで、前シリーズでは、数式を一切書きませんでした。

このシリーズでは、公式を使うために必要なことを書いていきたいと思っています。
壮大なテーマなので、落としどころをどうするか、着地点が見えないまま離陸してしまいました。
とりあえずできるだけのことをやっていきましょう。

公式とは

ウィキペディアでは、公式を『数学において公式（こうしき）とは、数式で表される定理のことである。』と定義しています。
しかし、これでは、公式とは何であるか、分からないのではないでしょうか。
公式の定義はいろいろあると思いますが、多くの場合、公式とは、理論的、または、実験的に得られた関係を、 数式で記述したもの、といえるのではないでしょうか。
また、その式が、社会的に認知されているということも公式と呼ぶためには必要になります。
すなわち、公式の構成要件（法律用語ですが）は、以下のようになります。

1. 数式で記述される
2. 理論、または、実験によって得られた
3. 公に認められている

上記の３つの条件を満たす場合には、それを公式と呼んでも良さそうです。
オーディオ技術で公式と呼ばれるものには、バスレフ型の共振周波数の計算式などの設計用の公式があります。
しかし、いったん公式が出来てしまうと、意味を知らずに盲目的に使う人が出てきます。
意味を知らずに盲目的に公式を使うと、たとえば、一桁結果が違っても気付くことができません。

公式は理解せずに使うべきではありません。

自分が公開している技術資料は、全て一般に使われている知識だけで書いており、それらを読むのに音響工学の専門知識は必要ありません。
ところが、なぜか、そのほうが難しいと感じる人は多いと思います。
おそらく、代入するだけで何かが出てくる公式を見ると、分かったような気になる人が多い、ということでしょう。
このサイトにある式は、電卓で計算するわけにはいかないもので、そのために、計算プログラムを公開しています。

これは、マイナーオーディオ講座なので、自分に理解できない公式は使わず、一般的な物理知識だけで展開します。

公式を見てみましょう

では、実際に公式を見てみましょう。
たとえば、FostexのCRAFT HANDBOOKには、密閉型エンクロージャ容積を決めるための以下のような公式があります。

但し、Fostexはこのページで使っている国際規格のSI単位ではなく、何十年も前のCGS単位と容積にはリットル単位を使っているので 混乱を避けるため、このサイトでは、以下のように記号を変えます。 Fostexでは実効振動半径にaという記号を使用していますが、こう書くと実効振動面積(area)と誤解しやすいので、r(radius)という記号を使用します。

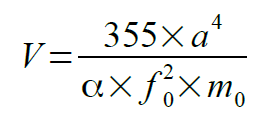
	Fostex		このサイト		備考
	記号	単位	記号	単位
実効振動半径	a	cm	r	m
実効質量	M0	g	m0	kg
容積	V	l	V	m3

この公式を使えば、適切な容量が求められるのでしょうか？
ここで疑問が浮かびます。
そもそも適切な容量とは何でしょうか？
(1)フラットに再生できる
(2)フラットではないが、まあ許せるくらいの低域の落ち方である
(3)低域は劇的に落ちるが、トーンコントロールなどで補正可能な落ち方である。
一般的にはこんなところが想像できますが、初心者は、(1)を目指すでしょう。
公式に使われている記号やパラメータの意味が分からなくても、電卓を弾けば数字が出てきます。
ここに大きな問題があります。

それは、さておいて、次回以降、しばらくはグループ(A)について検討してみましょう。