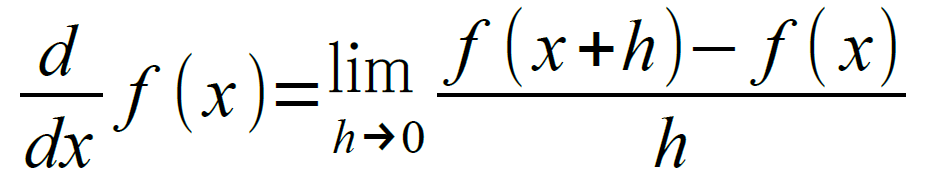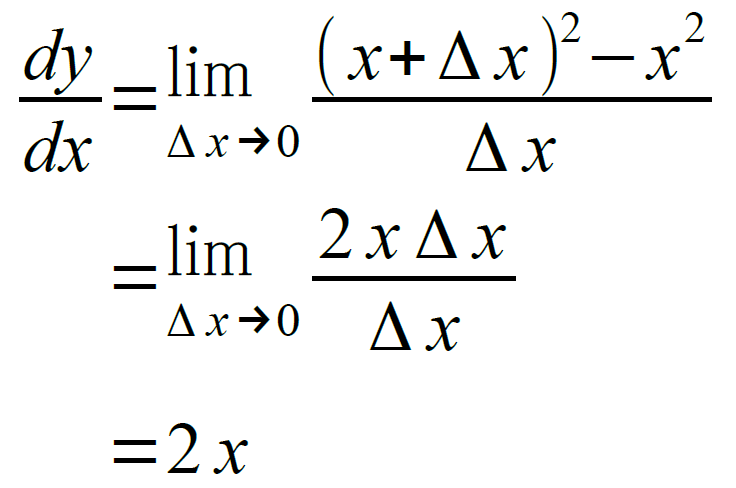はじめに

前回は、三角関数の加法定理を見てきました。
加法定理を導いた理由は、三角関数の微分形を求めるためです。
微分を理解することは、三角関数を役立てるためには必須です。
三角関数だけでなく、世の中の現象の過渡状態を表現するためには、微分は絶対に必要です。
微分のことを英語で"derivative"と表現します。
投資やトレーﾄﾞの用語でもデリバティブがあります。
このデリバティブは、微分とは違う意味で使われていますが、微分について知っていれば、ばるほど、と思うことでしょう。
ということで、今回は、微分についておさらいします。
教わっていなくても、どのようなものか概念を知っていると役に立ちます。
微分なんか何に使うのか？と思ってもこらえてください。
必ず役立てることができるます。

変化の割合

高校で微分を教わる少し前、中学のときに、『変化の割合』という概念を教わります
変化の割合をごく直感的に表現すると、横軸の値の変化に対する縦軸の値の変化となります。
このときに重要なのは、グラフがまっすぐでない場合には横軸の値の変化の大小によって、そのときに縦軸の値の変化量が変わることです。
これを図で確認してみましょう。

この図において、横軸の値xがx+Δxに変化したときに、縦軸の値yはf(x)からf(x+Δx)に変化します。
yの変化量をΔyとすると、このときの変化の割合が、Δy/Δxということになります。
ここで、Δ（デルタ）というギリシャ文字は、変化や差を表したいときによく使う文字で、例えばΔxというのは、xの変化量という意味になります。
これが、微分を定義するための前提の知識になります。
高校入試のときに勉強された方が多いのではないでしょうか。

微分の定義

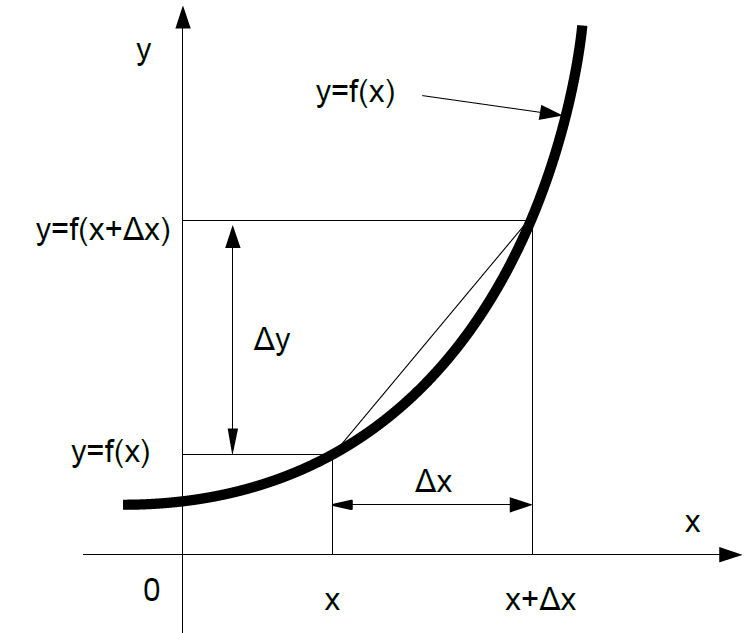
上に見た変化の割合において、横軸の変化の量を極限までゼロに近付けたときの変化の割合の値を、その点における『微分係数』といいます。
これを、数式で表現してみましょう。ここでは、高校で教わる表現として、Δxの代わりに、hという文字を使います。

これが、微分係数の定義です。

この式を見てもピンと来ないと思いますので、二次関数の微分の例を導いてみましょう。
ここでは、いちばん簡単なy=f(x)=x²という二次関数の微分形を求めてみましょう。

微分形を導く定義式を覚えている人は多数派ではないと思いますが、定義通りに導くことができます。
今回は、三角関数の微分形を導くために、微分係数の定義について説明しました。
次回は、三角関数の微分係数を求めましょう。