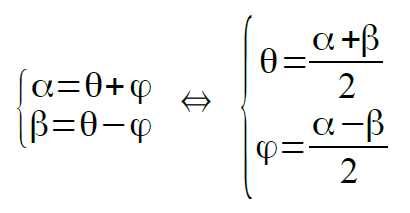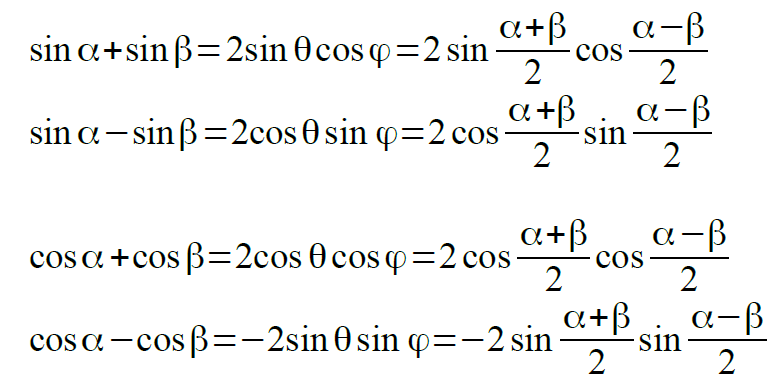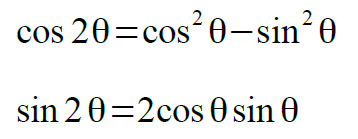はじめに

前回は、行列の掛け算を見てきました。
そして、連立運動方程式の行列を使った表現を紹介しました。
連立の運動方程式も、行列を使うことで、とても見やすくなりましたね。
行列を使うことによって、変数をどんどん増すことができます。
自分も行列を知らなければ、多自由度バスレフの研究はできませんでした。
多自由度バスレフなんて、自分の知らない世界だ、と思われる方が多いようですが、紐解けば、 基礎となる部分は、高校で教わった内容です。

今回は、いよいよ三角関数の加法定理に入ります。
加法定理が終わればつぎは三角関数の微分です。
微分なんか何に使うのか？と思ってもこらえてください。
必ず役立てることができるます。

回転変換から加法定理へ

前々回に、行列をつかったベクトルの回転変換について説明しました。
そのなかで、単位ベクトルを回転する行列を見つければ、任意の点を回転する変換行列が見付けられることを説明しました。
したがって、回転変換する行列を覚える必要はありません。
都度図を書けば、すぐに回転変換行列をみつけることができます。
自分は、公式の類をほとんど覚えていないので、都度導けるようにしています。
信じられないかもしれませんが、バスレフの共振周波数を求める計算式も、都度導いています。
そして、一応、ウェブなどで調べて確認するようにしています。
この方法は一見すると効率が低そうですが、何もないところでも研究できるので重宝します。

では、回転変換を再び見て行きましょう。
座標(x,y)をθラジアン回転変換して、移動した先の座標を(x',y')とすると次式のようになります。

さらに、(x',y')をφラジアン回転変換して、移動した先の座標を(x",y")とすると次式のようになります。

すなわち、次式が成り立ちます。

また、極座標のところで見てきたように、θラジアン回転してからφラジアン回転する変換は、θ+φラジアン回転するだけなので、

となります。

ここまでで、もう加法定理が導けるようになりました。

計算してみると、

と簡単に導けてしまいました。

加法定理はたったこれだけのことです。

学校では、θ-φの場合も公式のように出てくると思いますが、自明なので暗記する必要はありません。
最初にグラフを見て確かめた、sin(-θ)=-sin(θ)とcos(-θ)=cosθ の2つが分かっていれば、加法定理が、引いた場合でも同じです。
下記も実際に確かめてみてくださいね。

加法定理の拡張

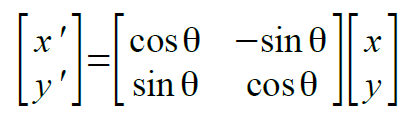
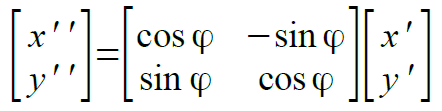
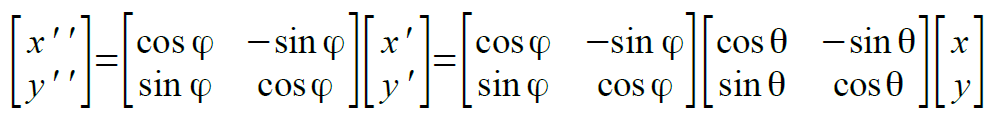
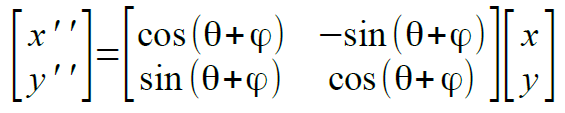
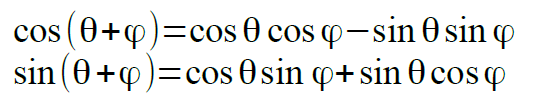
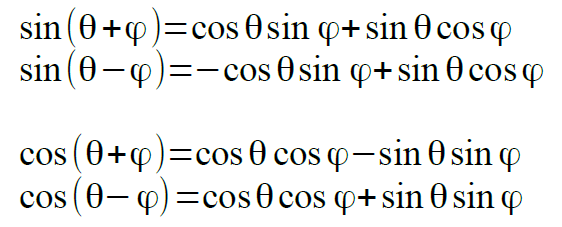
すでに、sin(θ+φ)とcos(θ+φ)の2つがどうなるかを見てきました。
これだけでも便利なのですが、α=θ+φ,β=θ-φとおくとまた別な便利な形の式を導くことができます。
すなわち、以下のように変数を置き換えます。

これを加法定理の基本形に代入して整理すると、

と別な形も導けてしまいました。

さらに、θ=φの場合を計算すれば、
と、こんな形も導くことができました。
くれぐれもこんな式を覚えようとしないでくださいね。必要なときに導くようにしましょう。

ひととおり勉強すると、高校で学ぶ数学の復習に役立つと思いますので、次回以降もお楽しみください。