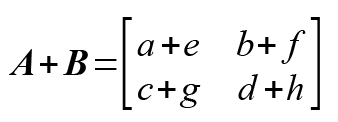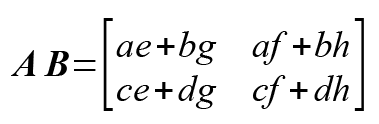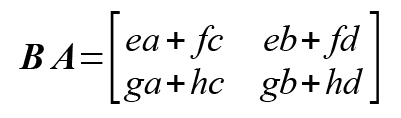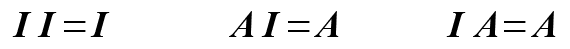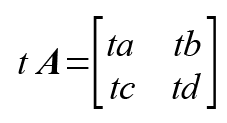はじめに

三角関数の理解のために、前回は、極座標表示と回転変換について書きました。
回転変換を説明するために、ベクトルと、行列についても書きました。
学校では、このような順番では説明されないとおもいますが、数学の本質は、すべてが結びついていることです。
ですから、学校の知識を実際に使おうとすると、このように、全く関係なさそうな内容を総動員することになります。
学校の定期試験のように、項目ごとに別々に覚えただけではなかなか役立てることはできません。
このオーディオ講座では、オーディオ趣味のために三角関数を勉強したら、知らない間に、総合的に理解していたということを目指そうとおもいます。
すべての公式は、定義から導けるようになります。
ということで、今回は、ベクトルと、行列のさわりを覚えましょう。

ベクトル

社会生活を営むためにいろいろな数字を使います。
たとえば、CDの値段が2,000円だったとか、ガソリンを10リットル買う、というように数字をふつうに使います。
これらの数字は、数学的には、スカラー量というものです。
スカラー量は、指し示している対象の規模の大小を表すものです。
これに対して、規模の大小だけでは、説明が不十分な量があります。
たとえば、歩いて移動する場合などです。
歩いて1km離れたところに行くにしても、それだけでは、どこに行けるのか分かりません。
つまり、距離だけでなく方向がわからなければ、十分に説明できない場合があるということです。
このように、規模に加えて方向を表すことができるのが、ベクトルというものです。
ベクトルについて深く追求すると、書ききれないので、まずは、2次元のベクトルを理解しましょう。

2次元の直行座標系では、ベクトルは、下記のように書きます。

sは、ベクトルを表します。
ベクトルは、このように太文字にしたり、上に矢印を付けたりして表しますが、論文などでは、このように太文字で書かれるのが一般的です。
xとyは、太文字になっていないことに注意してください。
xとyは、それぞれの方向の量です。正の数であっても、負の数であっても、ゼロでも、かまいません。
複素数を使うことも理論的には可能ですが、複素数は、そのものがベクトルの要素を持っているし、自分は、まだ、 ベクトルのコンポーネントに複素数を使う必要性を感じたことがないので、とりあえずは、ベクトルの要素は実数であるとして考えましょう。
xが負の数の場合は、左向き、正の数の場合は右向きになります。
同じように、yが負の数の場合は下向き、正の数の場合は上向きなので、ベクトルは、上下左右、斜め、と好きな方向を向くことができます。

行列

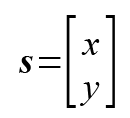
行列は、ベクトルの計算を行うときに便利なツールです。
ベクトルに、実数を掛けても、大きさが変えられるだけで、方向は、正の数をかけたときに同じ方向、負の数をかけたときに逆方向、というようにしか変えることができません。
行列を使えば、好きな方向に角度を変えることができます。
行列を使うと、多くの計算を簡単な式で表現できるので、多自由度バスレフ型の運動方程式にも行列を使った式が多く使われています。
普通の数字のように行列を使えるようになりましょう。

難しいことは置いておいて、実際に行列の計算をやってみましょう。
行列において、横方向の並びを、『行』とよび、縦方向の並びを『列』とよびます。
縦横それぞれ無限に拡張できます。
横を2行、縦を1列にしたものは、ベクトルと同じです。

高校では、3行3列までしか使わないとおもいます。
圧倒的に多く使うのが、2行2列ですので、ここでは、2行2列に限定しましょう。
行列は、通常、アルファベット大文字の太字を使います。

のとき、足し算は、
となります。各要素を足すだけなので簡単ですね。引き算は同様です。

掛け算は、面倒です。
これが、2行2列の行列の掛け算になります。
ちなみに、同様に計算すると、
となるので、ABとBAとは通常は等しくないことがわかりますね。
だから、行列は、右から掛けるとか、左から掛けるというようにわざわざ表現します。

行列の割り算は、逆行列を掛けることとして定義されます。
逆行列とは、数字の逆数のようなもので、その行列を掛けると、『単位行列』になる行列です。
単位行列とは、数字の1に相当する行列で、これをIと各と、2行2列の行列では、
となります。
実際に計算すると確かめられるとおり、
となります。

行列にスカラー量を掛けることもできます。これは、各要素にスカラー量を掛けると定義され、
となります。

ものすごく駆け足で見てきたので、次回は、補則します。