多自由度バスレフ型スピーカーシステムの研究開発
物理モデルに基くシミュレーションソフトウェア開発
|
Project MCAP-CR 多自由度バスレフ型スピーカーシステムの研究開発 物理モデルに基くシミュレーションソフトウェア開発 |
|
前回は、三角関数のうち、単位円を使ったサイン、コサイン、タンジェントの定義について書きました。
三角関数は、この部分だけ暗記しても、役立つことは殆どありません。
どのように役立つのか、書ききれないくらい、有効な使い方ができるものです。
慣れてしまうと、水や空気のように、不可欠であり、すべての前提として使うものです。
学校では、三角関数に関する公式をたくさん教わりますが、これらを頑張って覚えるのは、効率のよい勉強法ではありません。
どのように使われていくかを実感として頭に入れてゆけば、公式を覚える必要はありません。
すべての公式は、定義から導けるようになります。
自分にも経験がありますが、試験を受けたとき、暗記した内容は、忘れてしまうものです。
多少の時間のロスはありますが、記憶する部分を最低限にとどめ、試験中に公式を導けば、ほんの少しの間違いですべてを失う危険は避けることができます。
公式を丸暗記するというようなリスク管理ができていない方法で、試験に望むのは、バクチと一緒です。
すべてを失うリスクを避けながら、確実に抑えたポイントをかせぐことが、生涯にわたって大切なことです。
今回は、三角関数の微分を理解するために必要な、極座標と回転変換について書きます。
これらのポイントを抑えてゆけば、三角関数は、水や空気のように不可欠なものとして感じられると思います。
水や空気のように感じられるようになれば、もう、それ以上暗記する必要はありません。
三角関数という概念を使うと、極座標という考え方が理解できるようになります。
通常は、横方向をx、縦方向をyとした直交座標を使って、平面上の任意の点を(x,y)のように座標で表示します。
多くの場合、直交座標だけでも使えますが、極座標を使うことができれば更に便利です。
直交座標と極座標との関係を図3に示します。
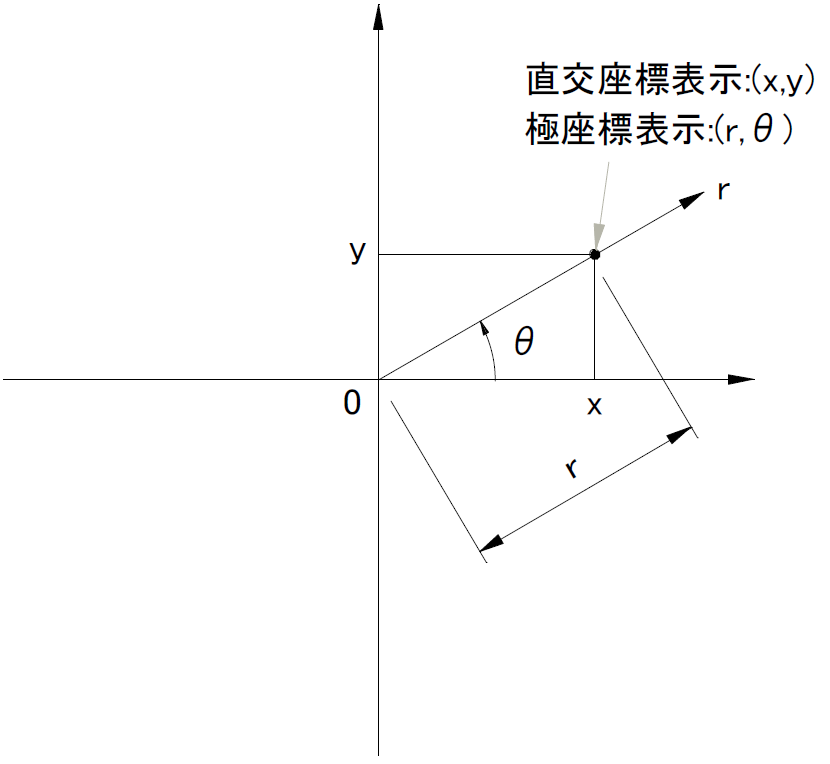
図3を見ただけで、以下の関係がわかると思います。こういうものを公式として丸暗記する必要はありません。図を数式として記述しただけです。

図3の点(x,y)を原点を中心として左方向にΦ回転させると、回転後の座標はどうなるでしょうか?
極座標表示であれば簡単ですね。
(r,θ)→(r,θ+Φ)
に移動します。
これが直交座標表示だったらどうなるでしょうか?
直交座標系だと少し面倒です。
しかし、少し工夫すると簡単に覚えることができます。
少し飛躍するようですが、回転変換は、行列で表現します。
行列というのは、ベクトルを拡張したようなものです。
高校1年生で、三角関数を教わるときには、多分、行列もベクトルも教わっていないと思います。
しかし、三角関数を理解するには、行列とベクトルとを知っておく必要があります。
まず、行列を使った回転変換を見てみましょう。
ベクトルと行列とは、次回以降に少し詳しくみることにして、まずは、結果を見てみましょう。
3回勉強してみてわからなければ、いったん先に進め、ともいわれます。
順番は入れ替わりますが、最初に回転変換行列をみてみましょう。
回転変換とは、平面上のある点を中心として、その平面上での特定の点の座標を決められた角度だけ、回転した位置に座標を移すことです。
回転の中心は、一般的には任意ですが、多くの場合は、原点を中心にとります。
原点以外を中心とする場合には、式は変わりますが、やっていることは同じです。
回転変換を表すのに行列を使う理由は、そのほうが表現しやすいからです。
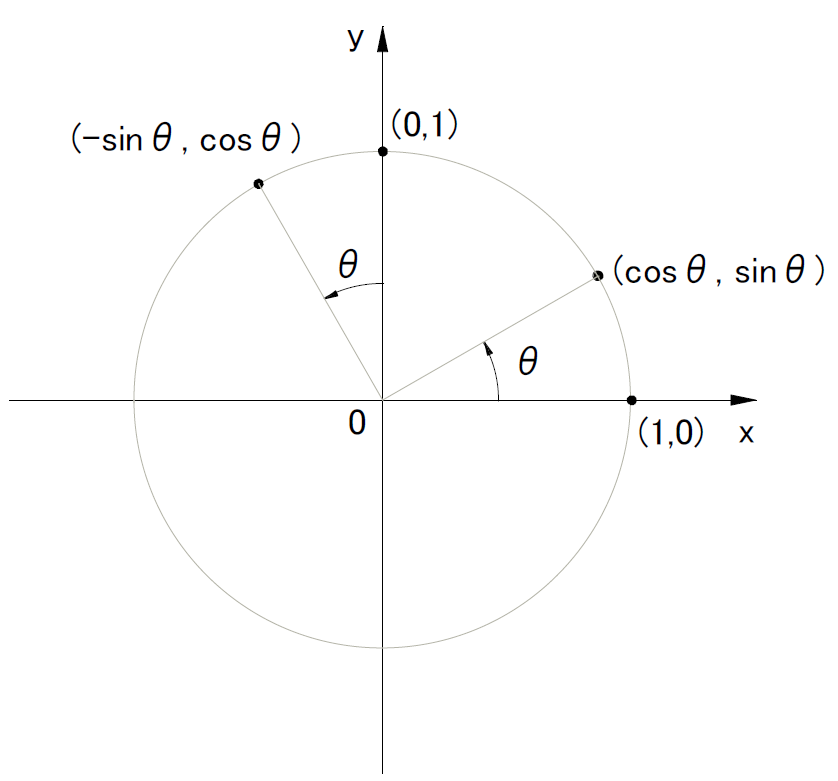
回転変換行列を見つけるために、軸方向の単位ベクトルを回転させてみます。
図4は、x軸方向の単位ベクトルの終点(1,0)とy軸方向の単位ベクトルの終点(0,1)を、原点を中心に回転させたものです。
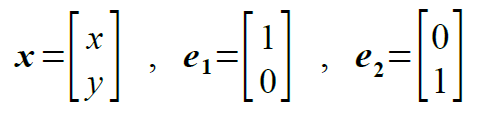 (8)
(8)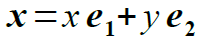 (9)
(9)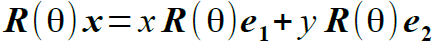 (10)
(10)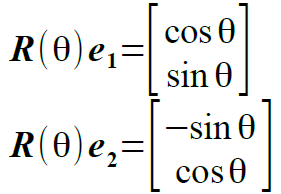 (11)
(11)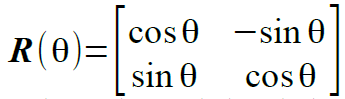 (12)
(12)