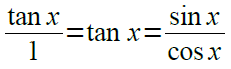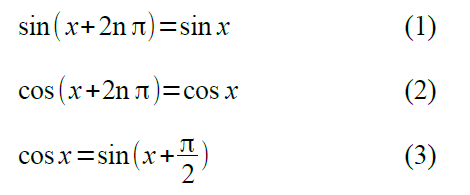はじめに
前回は、オーディオ機器の評価のために、稀に使われるブラインドテストと、その結果についての超概要を書きました。
まとめると、
完全なブラインドテストを実施するのは不可能に近い
ブラインドテストであっても、公正さが担保されるわけではなく、結果を誘導することは可能である
ブラインドテストの結果は、統計手法に基いて、その結果が偶然だったのか、必然だったのかを判定する
統計手法で、結果が必然であったと判定されても、それだけで、因果関係を証明することはできない
ブラインドテストのレポートを読むにあたっては、4要件に注意する必要がある
といったところです。
統計処理で、有意差のあることが示せない場合は、有為差ありという仮説を棄却する=有為差なし ということになります。
逆に、有為差がないことを示せない場合には、有為差なしの仮説は棄却され、有為差ありとなります。
検定の手法については、高校までで教わる内容を超えるので詳細は書きませんでした。
高校では、正規分布する対象に限定して、検定を教わりますが、一般的にはもう少し拡張が必要です。
分布の拡張については、高校の範囲を超えるので、これ以上すすめるかどうかは後で考えます。
今後しばらくは、三角関数について、書きます。
受験勉強と同じでは、味気ない内容になってしまうので、少し違う観点から書いてゆきます。
学校で教わる内容が、どう役立つのかについて書いていきます。
三角関数
三角関数といえば、サイン、コサイン、タンジェントという用語を思い出します。
これらは、高校で教わる内容ですが、その後、使っている人はどれくらいいるのでしょうか。
『受験が終わったらそんな知識は使わないよ』と思っている人も多いかもしれないし、そういう発言を聞くと、勉強する気もなくなるかもしれません。
自分は、学校で教わる知識は一生ものだと思います。
すくなくとも、三角関数を知らずに、オーディオ評論をする人はいないはずです。
三角関数は、どういうところで使われるのでしょうか?
使い道のうち、オーディオに関するものの、そのまた一部を書いてみます。
- 周波数を表現する
- 歪率を表現する
- 位相の違いを評価する
三角関数は、他にも無限に使われていますが、オーディオ趣味に関するものの多くは、上記の内容に帰結すると言ってもいいのではないでしょうか。
歪率と位相のはなしは、少し専門的な感じも受けますが、周波数を表現できなければ、オーディオは何もすすみません。
ということで、今回は、三角関数の定義からはじめましょう。
三角関数の定義方法は種々あるようなので、ここでは、『単位円』を使った定義方法について書きます。
自分が高校のときは、直角三角形を使った定義から入りましたが、それでは、その後に勉強する『信号処理』の手法に直接結び付きません。
単位円から始めると、後に勉強する『複素数』の概念にも繋がります。
単位円と三角関数
単位円とは、平面上のある1点から距離"1"はなれた点の集合です。
多くの場合、中心を原点にとるので、原点を中心とした、半径"1"の円、と書いても良いでしょう。
単位円の中心から放射状に角度"x"の直線を引きます。
その直線と単位円の交点を、角度"0"の直線に垂直に下ろした位置がcos(x)、角度直角の直線に垂直に下ろした位置がsin(x)です。
そして、単位円の右端または左端を通り、角度直角の直線に下ろした位置がtan(x)です。
ことばでは分かりにくいので、これを図1に示しました。
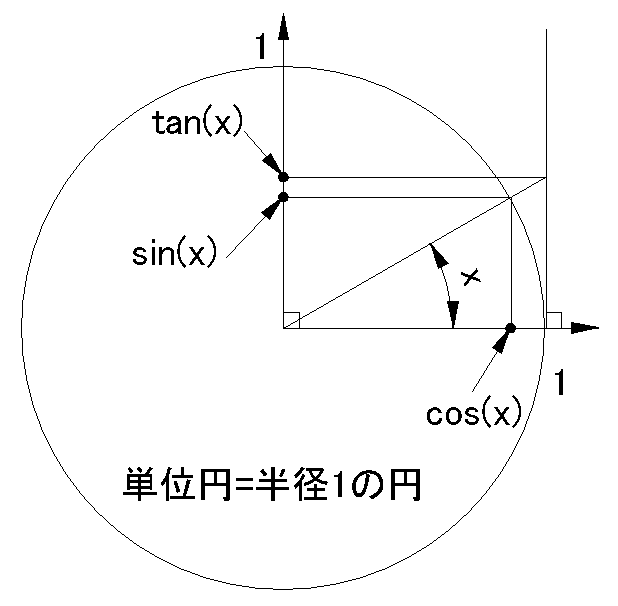
図1.単位円
|
|
図1では、xが0と直角との間ですが、直角より大きくても構いません。
また、xは負の数でもかまいません。
すなわち、xは実数であればどのような数字でも、三角関数が定義できてしまいます。
角度360度で1周しますので、1周するごとに元に戻ります。
この、『
1周するごとに元に戻る』ということが三角関数の非常に重要な性質です。
また、単位円の半径が1であることに注意して、tan(x)、sin(x)、cos(x)それぞれの関係を見ると、
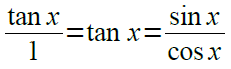
という関係があることがわかります。
これで、公式をひとつ暗記しないで済みますね。
角度の表示方法
一般的な角度の表示には、度、分、秒という単位を使います。
直角は0度、1周すると360度という表示で、お馴染みのものです。
しかし、三角関数を使うには、角度を度という単位で扱うのは少し不便です。
まず、単位円を定義したことを思い出してください。
単位円は、半径1の円です。
この円の円周の長さは、いくつでしょうか?
直径に円周率を掛けると円周の長さになりますので、単位円の円周の長さは、
2×π=2π
となります。これが1周分の周長になります。
直角分ならこの1/4なので、π/2となります。
円に沿った周長は、中心角に比例するので、単位円の周長で角度を表すことができます。
そこで使用されるのが、ラジアン[rad]という単位です。
ラジアンの次元は、無次元です。すなわち、単位はありません。
ですから、角度がπというように表示します。
角度が30度なら、ラジアンで表すと、30/360*2π=π/6というように、通常の度という単位から、ラジアン表示に簡単に変換できます。
よく使われるのは、π/6=30度、π/4=45度、π/3=60度、π/2=90度 といったところです。
なぜ、ラジアンを使うと便利なのかというと、理由はいろいろありますが、そのうちのひとつは、x[rad]がゼロに近いところでは、
x≒sin(x)
となることです。これは、意外に多く使う定理ですので、覚えておくと便利でしょう。
サインとコサインの覚え方
サインとコサインの覚え方については、図1に示しましたが、それだけでは、直角三角形の図で覚えるのと大差ありません。
折角単位円に基く定義を使うのですから、少し違った形で覚えましょう。
下の図2を御覧ください。
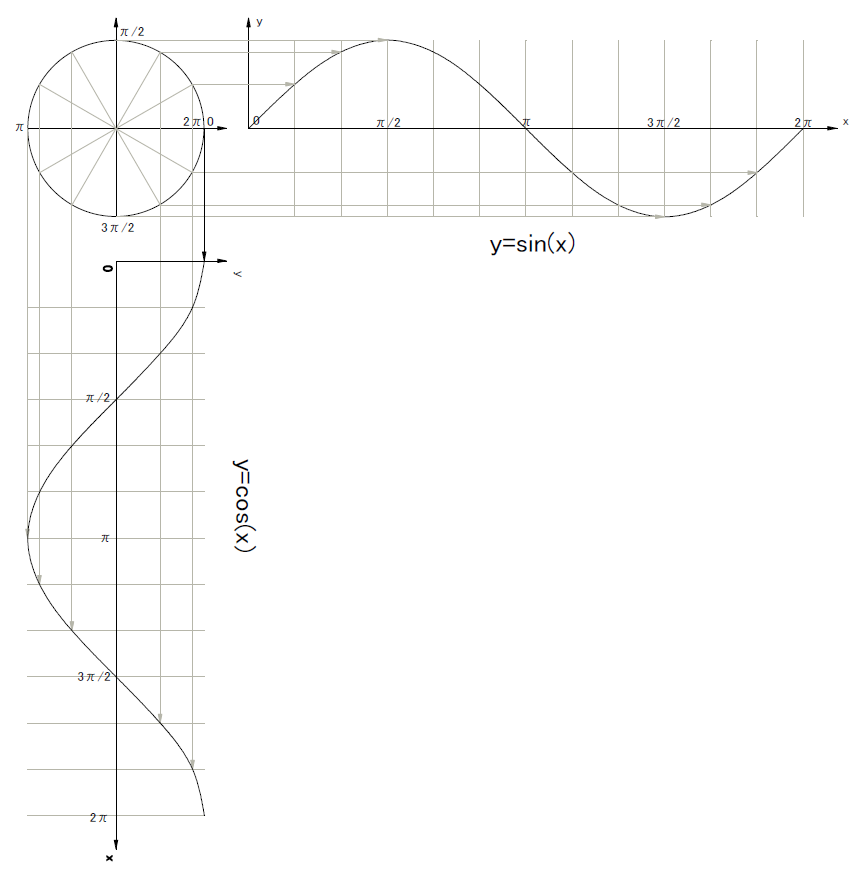
図2 サインとコサインのグラフ表示
図2は、単位円上の点を、サインとコサインのグラフに射影して表示したものです。
サインは、単位円上の縦軸の値を射影したもので、図2の右側のグラフです。
コサインは、単位円上の横軸の値を射影したもので、図2の下側のグラフです。本体は、このグラフを反時計回りに90度回して表示すべきですが、
覚えやすいように、このような表示をしています。
このように書くと、サインとコサインの重要な性質がビジュアルになります。
- サインもコサインも1周(2π=360度)すると元に戻る
- サインもコサインも、何周しても同じ形である
- コサインは、サインを1/4周(1/2π=90度)進めただけで、同じ形をしている
このように書くと、以下の公式は、覚える必要がないことがわかります。
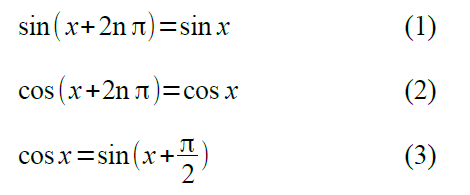
但し、n=1,2,3,...
数式で書くと、ピンときませんが、図2と比べると感覚的にわかりますね。
ここで、(1)式、(2)式の"n"は『何周しても』ということを意味しています。わかりやすいように、n=1,2,3,...と書きましたが、マイナス
(逆向きに回る)であっても良いわけです。
このように、公式を覚えていなくても、本質的なことを知っていれば、公式は書けるので、公式なんか覚えようとしてはいけません。
その公式の意味を考え、理解して、いつでも導けるようにしておくほうが、はるかに効率的です。
公式を覚えようとして、惜しい間違いがあったとき、どうなるか想像してください。
当然0点になりますね。公式の丸暗記に時間を使うことは、無意味ということです。
公式の意味を理解していつでも導けるようになることは、受験で使えるテクニックにもなります。
また、図3をよく観察すると以下のことにも気付きます。
sin(-x)= -sin x
cos(-x)= cos x
これらの式は、単位円上の点を左回りするか、右回りするかという違いについての表現です。
正方向が左回り、負方向が右回りなので、sinは、逆回りすると、正と負とが入れ替わりますが、cosは、どちらに回っても同じになります。
これらも図を見て理解してしまえば、公式として暗記する必要のないことがお分かり頂けると思います。
次回は、三角関数の微分を覚えるための準備について書きます。