その6 - Calcへのモデルの実装

スプレッドシートにプロセスモデルを実装する例について書きます。
実装方法は無限にあるので、その中の一例であるとご理解ください。
実装するのは、プロセスモデルの離散化データ（一時遅れ+無駄時間モデルであれば(9)式など）、 ステップ応答をインパルス応答に変換する式、および、プロセスのインパルス応答を離散化式で表した (13)または(14)式です。

以下に実際の例について表現してゆきます。

まず、最初にプロセスのステップ応答を入力します。
ステップ応答は、ステップテストを実施することで、実際のデータから取得することができます。
ここでは、任意に作成してみます。
もちろん、ステップテストの結果を一時遅れ+無駄時間モデルや二次遅れモデルに同定しても かまいませんし、逆応答を定義してもかまいません。
ここでは、簡単のため、10ステップで定常に達する任意のモデルを定義します。
ゲインは、各応答値に掛ければ良いので、ステップ応答は、0から始まり、定常値を1とします。
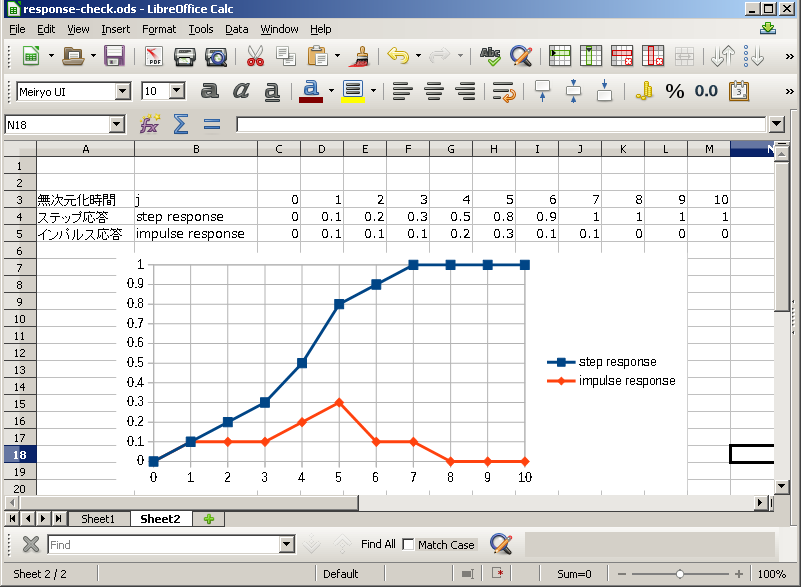
図6 プロセスの応答モデルとインパルス応答

この例では、C4からM4にステップ応答の値を入れます。
応答はどのような形であってもかまいませんが、C4は0、L4とM4は、1にすることが必要です。
定義したステップ応答モデルから、インパルス応答モデルをつくります。
インパルス応答モデルは、C5にゼロを入れ、D5にC5-C4を入力します。
そしてE5からM5は、D5をドラッグ＆ドロップして入力します。
すると、5行目がインパルス応答の値となります。

ここまでで、プロセスモデルの定義が終わりました。
プロセスの応答を更に細かくする表現するには、応答を定義する幅を広くとります。
この例では、n=10であり、また、この幅以内で定常に達する（(15)式）までしか表現できませんが、 これをn=20、n=50、...と広くることは可能です。
ただし、プロセス応答の幅を大きくするとスプレッドシートの動作が遅くなります。
幅を広くしても手順には変更がありませんので、ここではn=10とした例を載せます。

この応答を、(13)式として実装するためには、スプレッドシートを1行ではなく、n+1行使用します。
スプレッドシート上に展開したプロセスモデルの実装例を図7に示します。

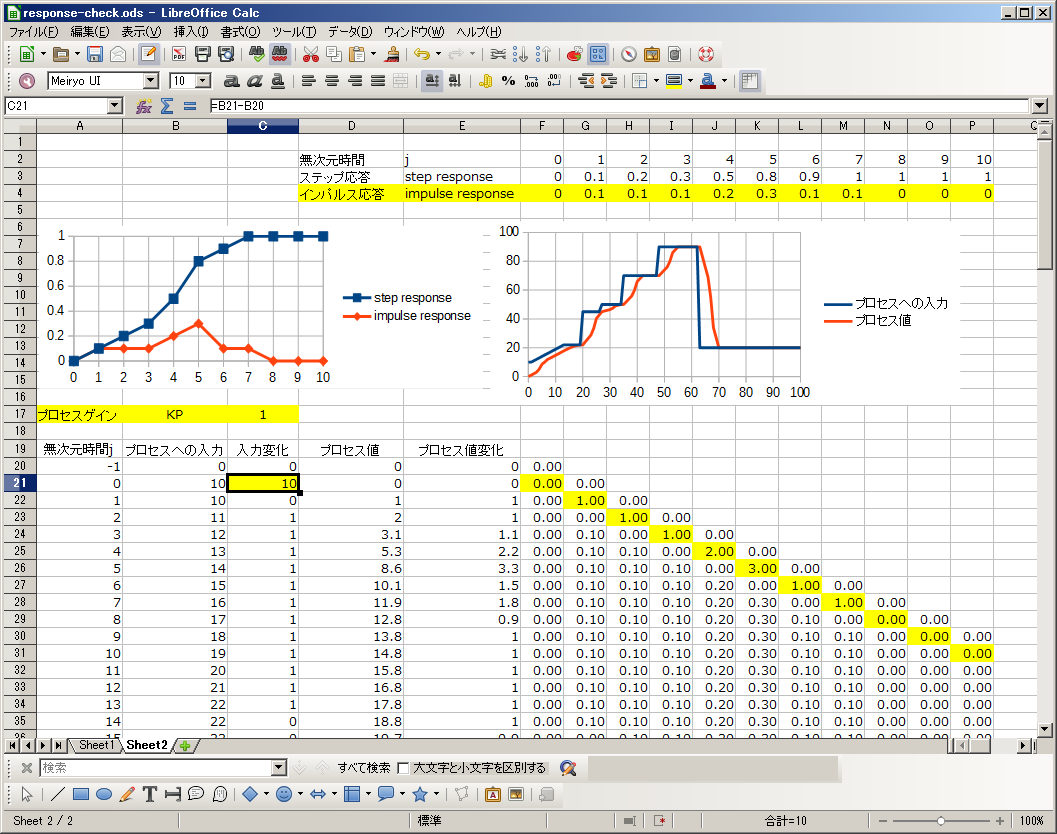
図7 プロセス応答モデルの実装

図7において、プロセスの応答モデルを、D2～P4に定義しています。
ステップ応答は、D3～P3で、ステップ応答を元に、インパルス応答を、計算した部分がD4～P4です。
そして、プロセスへの入力値の変化に対する応答である、(13)または(14)式を定義していきます。
この式を表現する方法にはいろいろありますが、 ここでは、表1の通り、図7の黄色に示した部分に入力してゆきました。
ここでは、分かりやすくするため、プロセスゲインの値K_Pを1としました。

表1　プロセス応答モデル式の実装

セル	計算式	備考
C21	=B21-B20	入力の変化分
F21	=$C$17*$C21*F$4	プロセスゲイン×入力変化分×インパルス応答の0番目の値
G22	=$C$17*$C21*G$4	プロセスゲイン×入力変化分×インパルス応答の1番目の値
H23	=$C$17*$C21*H$4	プロセスゲイン×入力変化分×インパルス応答の2番目の値
I24	=$C$17*$C21*I$4	プロセスゲイン×入力変化分×インパルス応答の3番目の値
J25	=$C$17*$C21*J$4	プロセスゲイン×入力変化分×インパルス応答の4番目の値
K26	=$C$17*$C21*K$4	プロセスゲイン×入力変化分×インパルス応答の5番目の値
L27	=$C$17*$C21*L$4	プロセスゲイン×入力変化分×インパルス応答の6番目の値
M28	=$C$17*$C21*M$4	プロセスゲイン×入力変化分×インパルス応答の7番目の値
N29	=$C$17*$C21*N$4	プロセスゲイン×入力変化分×インパルス応答の8番目の値
O30	=$C$17*$C21*O$4	プロセスゲイン×入力変化分×インパルス応答の9番目の値
P31	=$C$17*$C21*P$4	プロセスゲイン×入力変化分×インパルス応答の10番目の値

そして、各セルを下側の計算の最終行までドラッグ&ドロップしてセルを埋めてゆきます。
そして、E21に、”=SUM(F21:P21)”を入力します。このE21が、(13)式の値になります。
そしてE21を下側の計算打切位置までドラッグ＆ドロップしてゆけば、プロセスの動的な応答を計算できます。
更に、入力値を適当に決めれば、プロセスの動的応答を計算できます（図7の中の右側のグラフ）。
プロセスの応答は、この方法で、実装できることが確かめられたました。